随机森林是一个非常直观,理解起来也比较容易的Bagging算法。前面我们介绍过决策树,其最大的一个缺点就是容易过拟合。随机森林则是由若干决策树组成的模型,其思想就是“三个臭皮匠顶个诸葛亮”。比如下图,就是由9个决策树组成的一个随机森林,其中6个决策树预测值为1,三个预测为0 ,所以最终预测值取多数方:1。如果是回归问题,一般取所有决策树预测结果的均值。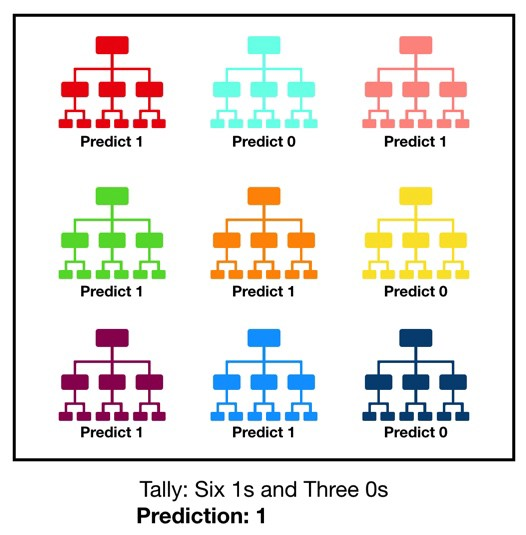
理解随机森林的关键点在于理解“相关度低甚至不相关的多个决策树组合在一起的效果好于其中任何一个决策树”。这里拿一个例子做论证(注:此例来自第一个参考文章),做一个游戏:使用一个均匀分布的随机数产生器产生一个数字,如果这个数字大于等于40,则算你赢,可以获得一些钱;如果小于40,则算你输,你需要给对方同样数额的钱。现在有三种玩法供选择:
- 玩法1(Game1):玩100次,每次的筹码是1元。
- 玩法2(Game2):玩10次,每次筹码是10元。
- 玩法3(Game3):玩1次,筹码是100.
你会怎么选哪一个?我们计算一下赢钱的期望值:
- $E_1 = (0.6*1+0.4*(-1))*100=20$
- $E_2=(0.6*10+0.4*(-10))*100=20$
- $E_3=(0.6*100+0.4*(-100))=20$
三种选择赢钱的期望值是一样的,那到底该如何选?我们做一个模拟:每种情况都模拟10000次,代码如下:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme()
# Game 1
simulations = 10000 # number of Monte Carlo Simulations
games = 100 # number of times the game is played
threshold = 40 # threshold where if greater than or equal to you win
bet = 1 # dollar bet for the game
# outer loop is Monte Carlo sims and inner loop is games played
sim_results_1 = []
for sim in range(simulations):
result = []
for g in range(games):
number = int(np.random.uniform()*100) # get a random number to see who wins
if number >= threshold:
result.append(bet)
else:
result.append(-bet)
sim_results_1.append(sum(result)) # sim_results_1 stores results for Game 1
print('Game 1 Mean: ', round(np.mean(sim_results_1), 2))
print('Game 1 Prob Positive: ', round(sum([1 for i in sim_results_1 if i>0])/simulations, 2))
print('\n')
# Game 2 (structure of code is same as above)
simulations = 10000
games = 10
threshold = 40
bet = 10
sim_results_2 = []
for sim in range(simulations):
result = []
for g in range(games):
number = int(np.random.uniform()*100)
if number >= threshold:
result.append(bet)
else:
result.append(-bet)
sim_results_2.append(sum(result))
print('Game 2 Mean: ', round(np.mean(sim_results_2), 2))
print('Game 2 Prob Positive: ', round(sum([1 for i in sim_results_2 if i>0])/simulations, 2))
print('\n')
# Game 3 (structure of code is same as above)
simulations = 10000
games = 1
threshold = 40
bet = 100
sim_results_3 = []
for sim in range(simulations):
result = []
for g in range(games):
number = int(np.random.uniform()*100)
if number >= threshold:
result.append(bet)
else:
result.append(-bet)
sim_results_3.append(sum(result))
print('Game 3 Mean: ', round(np.mean(sim_results_3), 2))
print('Game 3 Prob Positive: ', round(sum([1 for i in sim_results_3 if i>0])/simulations, 2))
# Histogram that shows the distribution of the Monte Carlo Results for 2 spending levels
fig, ax = plt.subplots(figsize=(8,6))
sns.distplot(sim_results_1, kde=False, bins=60, label='Play 100 Times')
sns.distplot(sim_results_2, kde=False, bins=60, label='Play 10 Times', color='orange')
sns.distplot(sim_results_3, kde=False, bins=60, label='Play 1 Time', color='pink')
ax.set_xlabel('Money Won by You', fontsize=16)
ax.set_ylabel('Frequency',fontsize=16)
plt.legend()
plt.tight_layout()
plt.savefig(fname='game_hist', dpi=150)
plt.show()模拟的输出以分布图如下:
# 代码输出
Game 1 Mean: 20.01
Game 1 Prob Positive: 0.97
Game 2 Mean: 20.2
Game 2 Prob Positive: 0.63
Game 3 Mean: 21.08
Game 3 Prob Positive: 0.61那可以看到赢钱的均值和即我们先前计算的期望值是一致的,三种玩法都接近20(Game x Mean),但赢钱的概率却相差很大,玩法1是97%,玩法2是63%,玩法3是61%。当然模拟次数再多一些,还有有一些变化。随机森林的思想和这个是一样的,里面包含的决策树的个数就是这里玩的次数。
另外,随机森林还有一个非常关键的限定条件:各个决策树之间不相关或者关联度很低。类比到上面的游戏中,我们的假设是产生随机数的算法是遵从均匀分布的,也就是产生1~100之间的数字的概率是完全相等的。如果不是,那上面第一种玩法1最优的结论就不一定成立了。而随机森林实现各个决策树之间不相关或者关联度很低是通过“两个随机”实现的:
- 数据随机:即每次只选取原始数据集的一个子集作为一个决策树的训练集,一般就是自助采样法(Bootstrap)。这是最核心的随机,主要是去除或者削弱各独立模型之间的相关性。
- 属性随机:属性随机化的好处在于让每个单独的基学习器不会过分关注在训练集中具有高度预测性或者描述性的特征。
通过两个随机,可以降低最终生成的模型的方差。而且通过这种方式生成的树一般也无需剪枝。Wikipedia上面的描述是这样的:
Each decision tree in the forest considers a random subset of features when forming questions and only has access to a random set of the training data points. This increases diversity in the forest leading to more robust overall predictions and the name ‘random forest.’
随机森林还有一个变种:Extra Trees。也称Extremely Randomized Trees,一般翻译为极限树,是随机森林的一个变种,进行了更彻底的随机,主要有两点:
- 训练各个决策树的时候使用全部数据集,而非一个采样的数据子集;
- 在选择决策树的拆分点的时候,均匀随机选择一个特征,而不是像随机森林那样根据信息增益或者基尼不纯度进行选择。
极限树的两个改动点在大部分情况下会进一步的降低方差,但可能会稍微增大一些偏差。
总结一下,随机森林的思路就是“群众的眼睛是雪亮的”,通过使用多个决策树组成一个“委员会”来进行预测或者回归,这些“群众”就是集成算法中的“若分类器”,他们相互之间没有关联度或者关联度低,而且一般在某一个点表现还可以。这点是通过“两个随机”去实现的,也是随机森林最核心的地方。
References:
 NYC's Blog
NYC's Blog 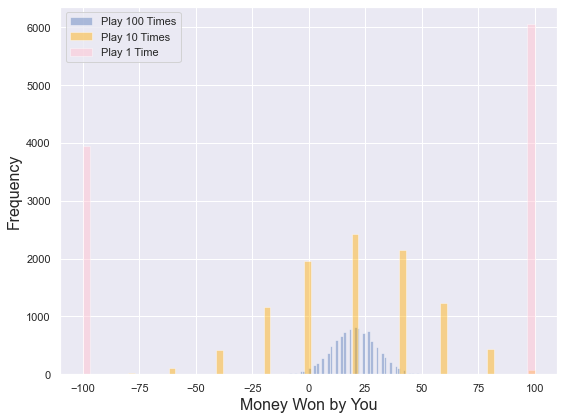
评论已关闭