最近准备整理一下之前关于集成学习的学习笔记,写一个关于集成学习的系列文章,毕竟目前用的比较多的机器学习算法基本都属于集成学习,整理一下,也算温习一下。有些笔记时间比较久了,里面的一些引用来源找不到了,所以有些引用可能附不全,敬请谅解。目前确定的几篇包括:
- 集成学习介绍(1)——Boosting && Bagging
- 集成学习介绍(2)——AdaBoost
- 集成学习介绍(3)——Random Forests
- 集成学习介绍(4)——GBDT
- 集成学习介绍(5)——XGBoost
- 后续待定...
后面可能会根据时间补充一下其它一些现在也比较流行的算法,比如LightGBM。
本文是第一篇。
集成学习(ensemble learning)是将多个基学习器(base learners)进行集成,得到比每个单独基学习器更优的强学习器(strong learner)的方法。每个用于集成的基学习器都是弱学习器(weak learner),即性能只比随机猜测好一点点或只在某些方面表现好一点的学习器(classifiers that produce prediction that is slightly better than random guessing)。
那如何保证多个弱学习器集成在一起会变的更好,而不是更差呢?即如何实现“1+1>2”的效果呢?这对弱学习器提出了一些要求:
- 弱学习器的性能要有一定的保证,至少在某个方面要表现比较好。
- 弱学习器的性能要有一定的差异,即擅长点要有所区分,这样组合后才能集百家之所长。
根据训练数据使用方法的不同,集成学习可以分为三种:
- 提升法(Boosting):各弱学习器之间存在强依赖关系而必须串行生成的序列化方法,各个弱学习器在最终的强学习器中权重不同;
- 装袋法(Bagging):各弱学习器之间不存在强依赖关系因而可以同时生成的并行化方法,各个弱学习器在最终的强学习器中权重相同;
- 堆叠法(Stacking):融合提升法和装袋法的一种集成。
注意:
- 集成学习属于机器学习,但它只是一种训练思路,而不是某种具体的算法。一般把他划归到元学习(meta learning):关于学习的学习。
- Boosting/Bagging的所使用的弱学习器一般是同类型的。
Boosting
提升法的是通过改变训练数据的权重(或概率分布)来训练不同的弱分类器,然后组合为强分类器。下面是两个示意图: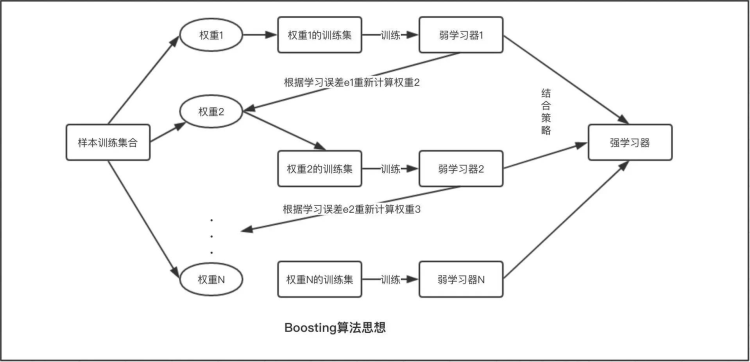
Boosting的重点在于取新模型之长补旧模型之短来降低偏差(bias),尽可能获得无偏估计。
Bagging
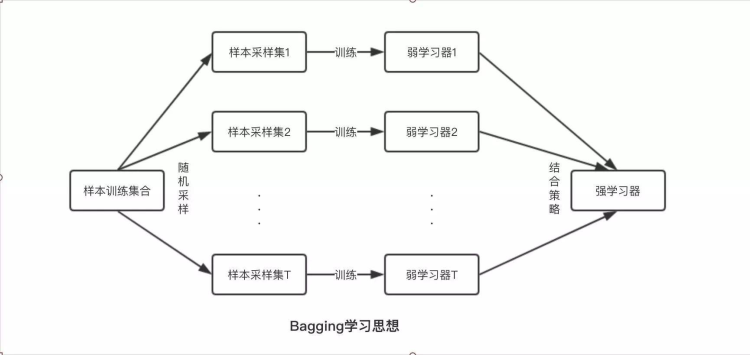
Bagging是Bootstrap Aggregation的缩写。Bootstrap也称为自助法,是一种有放回抽样方法。Bagging的的基本思想是对训练数据进行有放回抽样,每次抽样数据就训练一个模型,最终在这些模型上面取平均。具体算法如下:
- Step 1: Multiple subsets are created from the original data set with equal tuples, selecting observations with replacement.
- Step 2: A base model is created on each of these subsets.
- Step 3: Each model is learned in parallel from each training set and independent of each other.
- Step 4: The final predictions are determined by combining the predictions from all the models.
Bagging可以降低模型算法的方差,但并没有降低偏差的效果,所以也就没法提升预测的准确性,所以在选择弱分类器时要尽量选择偏差小的。
为什么Bagging能降低模型的方差?因为“如果对N个相互独立且方差相同的高斯分布取平均值,新分布的方差就会变成原始方差的 $1/N$”。Bagging采用独立有放回抽样得到N份数据,并训练得到N个模型,预测的时候最终会取这N个结果的平均(分类的话是取多数),这样就可以降低方差。
对比
下面对Boosting和Bagging做了一些对比:
| Boosting | Bagging | |
|---|---|---|
| 样本选择 | 每一轮训练集不变,但权重根据上一轮进行调整 | 从原始数据集中通过独立、有放回抽样获得 |
| 样例权重 | 根据错误率不断调整,错误率越大的样本权重越大 | 使用均匀抽样,各个样本权重相同 |
| 模型权重 | 每个弱分类器都有相应的权重,分类误差越小的分类器权重越高 | 各个模型(弱分类器)权重相同 |
| 并行计算 | 各个分类器串行生成,因为后面的分类器需要前一轮的结果 | 各个分类器并行生成 |
| 目标 | 主要为了减小偏差 | 主要为了减小方差,并且解决过拟合问题 |
| 适用场景 | 分类器比较稳定(即方差比较小)和简单(即偏差比较大) | 分类器不稳定(即方差比较大),且偏差比较小的 |
| 代表算法 | AdaBoost、GBDT、XGBoost | 随机森林 |
Stacking
除了提升法和装袋法之外,另一种知名度较低的集成方法是堆叠法。堆叠法(stacking)也叫堆叠泛化(stacked generalization),是层次化的集成方法,其思想和神经网络类似,只不过神经网络堆叠的对象是神经元和隐藏层,而集成方法堆叠的是同构或者异构的基学习器。
堆叠法先要用自助采样生成不同的数据子集,用数据子集训练第一层中不同的基学习器。第一层基学习器的输出再被送到第二层的元分类器(meta classifier)中作为输入,用来训练元分类器的参数。
堆叠法的思想和前两种方法有所不同。无论是提升法还是装袋法,其重点都落在单个模型的生成方式上,也就是如何训练出合适的基学习器,基学习器的形式一般是统一的。而堆叠法的重点在于如何将不同的基学习器的结果组合起来,研究的对象是让所有基学习器共同发挥出最大效果的组合策略。某种意义上说,堆叠法的训练数据不是原始的训练数据集,而是不同基学习器在训练数据集上的结果,起到的是模型平均(model averaging)的作用,提升法和装袋法都可以看成它的特例。正因如此,堆叠法除了被视为集成方法外,还可以看成是模型选择的一个手段。
以上这段摘自极客时间《机器学习40讲专栏》
关于偏差和方差
最后补充介绍一下偏差和方差这两个重要的概念。
一个机器学习模型的误差可分为两类:
- 经验误差(empirical error):又称训练误差(training error),指模型在训练集上面的误差;
- 泛化误差(generalization error):模型在测试集上面的误差。
其中泛化误差又可以分为三部分:
- 偏差(bias):表示算法预测值与真实值之间的偏离程度,刻画的是模型的欠拟合(under-fitting)特性。偏差大,说明模型欠拟合。
- 方差(variance):表示数据扰动对预测性能的影响,刻画的是模型过拟合(over-fitting)特性。方差大,说明模型过拟合。
- 噪声(noise):表示在当前学习任务上所能达到的最小泛化误差,刻画的是任务本身的难度。
用公式可表示为:
$$ generalization\_error = bias^2 + variance + noise $$
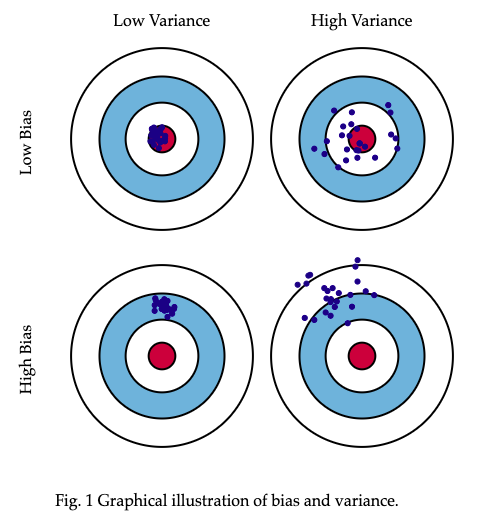
一般很难做到同时将偏差和方差都降到很低,只能在二者之间做权衡。下图中,靶心的红色是是预测正确的值,越往外,预测结果越差。四个图分别描述了误差和方差的高低情况:
上图来自:Understanding the Bias-Variance Tradeoff一文,关于偏差和方差的更多细节,也可以参考这篇文章。
 NYC's Blog
NYC's Blog 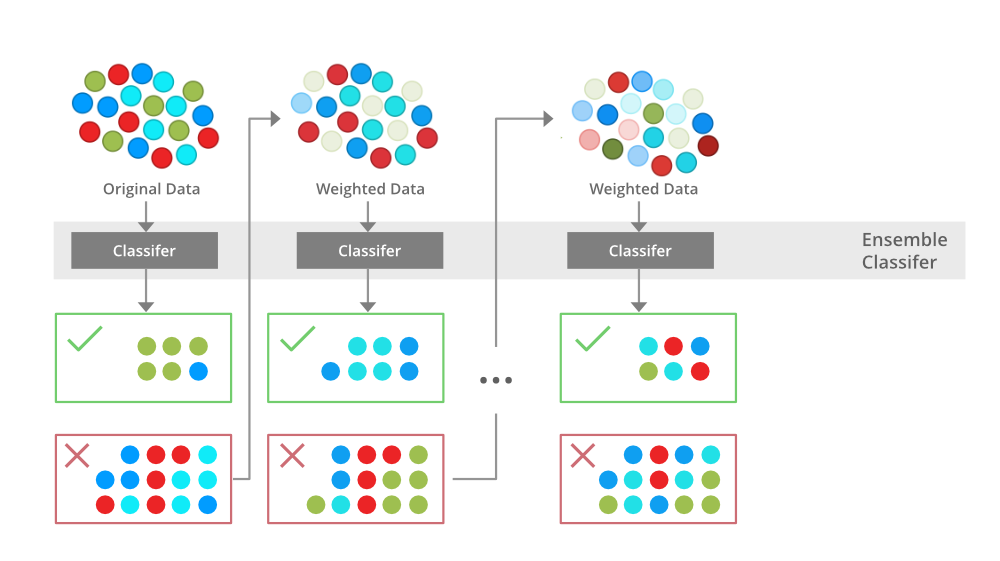

评论已关闭