概述

AdaBoost是Adaptive Boosting的缩写，即自适应提升法，是最成功的Boosting算法。具体算法如下：

Step1: Initialise the dataset and assign equal weight to each of the data point.
Step2: Provide this as input to the model and identify the wrongly classified data points.
Step3: Increase the weight of the wrongly classified data points.
Step4: if (got required results)
            Goto step 5
        else
            Goto step 2 
Step5: End

即初始的时候，赋予每个训练样本相同的权重；然后每次迭代后，增加分类错误样本的权重（数据集还是原来的数据集，只不过各个样本的权重变了），使得下一轮迭代时更加关注这些样本。

AdaBoost一般选用决策树桩（decision stump）作为弱学习器。所谓stump是指由一个决策节点和两个叶子节点组成的二叉树：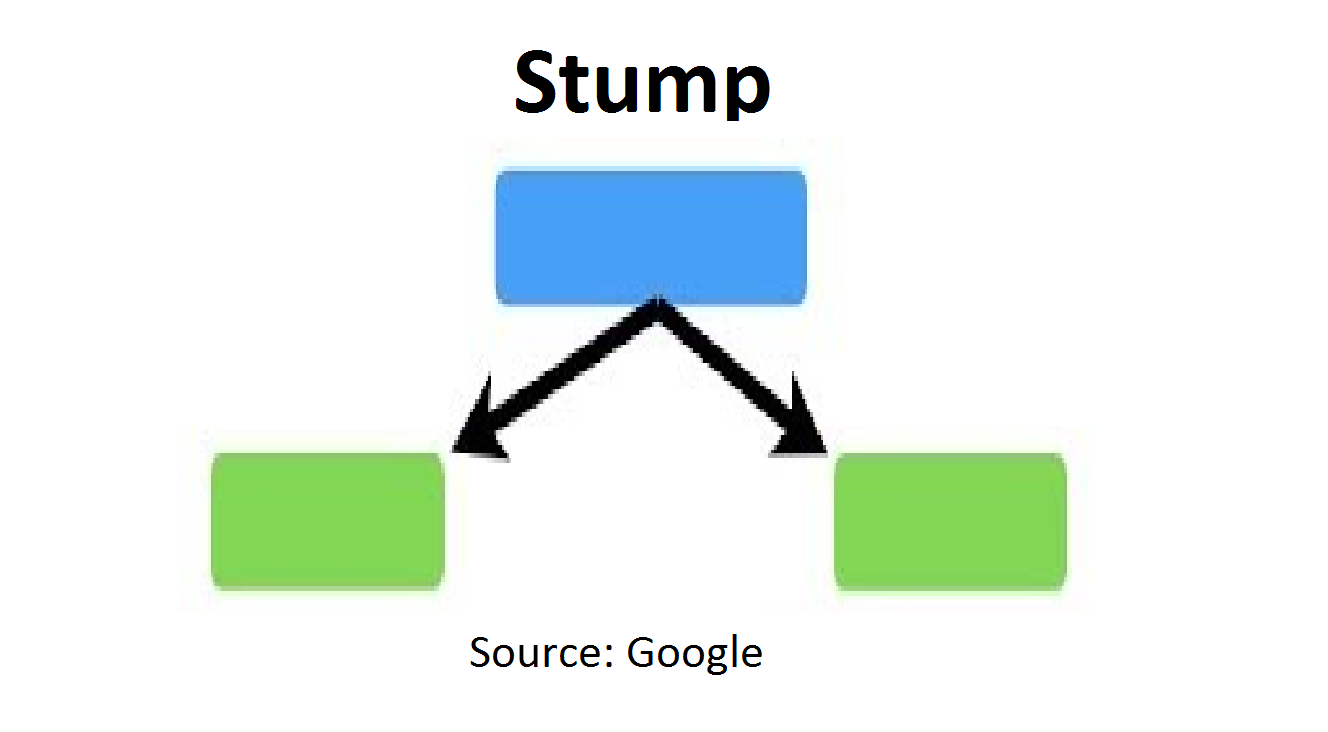
image.png

下图是一个二分类问题的学习过程示例，包含了三轮迭代：
image.png

算法

AdaBoost的算法描述如下：

image.png

下面进行解释。

  1. “输入”（Given）部分：输入训练数据集包含m个样本，其中$x_i$是属性，取值范围属于集合$X$(实数集的子集)，$y_i$是标签，取值是-1或+1.
  2. “初始化”（Initialize）部分：$D$表示带权重的样本（有时也用$w$表示），$D_i$表示第$i$个权重的样本。刚开始的时候，所有样本权重相同为$D_i = 1/m$.

  3. 然后开始循环：

    1. 使用权值分布为$D_t$的数据集，训练得到一个弱分类器$h_t$
    2. 计算$h_t$在训练数据上面的误差$\varepsilon_t$
    3. 根据训练误差$\varepsilon_t$计算出权重调整系数$\alpha_t$
    4. 更新所有训练样本的权重，用于下一次迭代
    5. 当训练误差比较低（比如错误率为0）或者弱分类器数目达到预先的设置值（超参控制），就停止循环
  4. 最终的分类器就是各个各个弱分类器的加权求和，如果是分类问题，就再加上符号函数$sign$（输入数据大于0，输出1；等于0，输出0；小于0，输出-1）.

如何计算训练误差$\varepsilon_t$？公式如下：

$$ \varepsilon_t = \frac {\sum_{i=1}^N\omega_iI(y_i \neq h_t(x_i))}{\sum_{i=1}^N\omega_i} $$

其中$I(y_i \neq h_j(x_i))$的含义是如果$y_i \neq h_j(x_i)$ 成立，则返回1，否则返回0。下面看个具体的计算例子：

  • 有4个样本的权重分别为：0.5，0.2，0.1，0.2，
  • 弱分类器预测的值分别为：1，1，-1，-1
  • 实际的真实值为：-1，1，-1，1
  • 则$I$的值分别为：1，0，0，1

于是有

$$ \varepsilon_t = \frac{0.5*1+0.2*0+0.1*0+0.2*1}{0.5+0.2+0.1+0.2} = 0.7 $$

有时也称$\varepsilon_t$为“total error”表示的是“所有错误分类的样本权重之和”，其实和上面的公式是一致的，因为权重一般是做过归一化的，所以分母里面的所有权重之和其实为1；而且分子中分类正确的样本的$I$值为0，也就是上面的公式可以简化为：

$$ \varepsilon_t = \frac {\sum_{i=1}^N\omega_iI(y_i \neq h_t(x_i))}{\sum_{i=1}^N\omega_i} \\ = \sum_{i=1}^N\omega_iI(y_i \neq h_t(x_i)) = 错误分类样本的权重之和 = total\ error $$

那权重调整系数$\alpha_t$的作用是什么呢？看个具体的例子。假设现在有3个$\varepsilon$值：0.3、0.5、0.7。则对应的$\alpha$的值如下：

$$ \alpha(\varepsilon=0.3) = \frac{1}{2}*ln\frac{1-0.3}{0.3} = 0.42365 \\ \alpha(\varepsilon=0.5) = \frac{1}{2}*ln\frac{1-0.5}{0.5} = 0 \\ \alpha(\varepsilon=0.7) = \frac{1}{2}*ln\frac{1-0.7}{0.7} = -0.42365 \\ $$

可以看到，当弱分类器的准确率为0.5时，其权重为0；准确率大于0.5（即错误率小于0.5）时，权重大于0；准确率小于0.5（即错误率大于0.5）时，权重小于0。所以，错误率$\varepsilon$越小，$\alpha$越大，即当前模型的表现越好，在最终的生成器中占的权重就越大。所以$\alpha$也称为“amount of say”、“Performance”、“Importance”，都指的是当前分类器在最终分类器中的权重。另外注意计算的时候有时使用自然对数（$ln=log_e$），有时使用常用对数（$log_{10}$）。

再来看最重要的部分：样本权重更新。在Boosting的迭代中，我们每次要找的是错误率比较低的弱分类器。为了方便我们沿用上面$\alpha(\varepsilon=0.3)$的计算结果，看下分类错误和正确时计算出来的权重值：

  • 当在样本$i$上预测正确（即$y_i = h_t(i)$），训练误差为0.3时，计算的新的权重如下：image.png
  • 当在样本$i$上预测错误（即$y_i \neq h_t(i)$），训练误差为0.3时，计算的新的权重如下：
    image.png

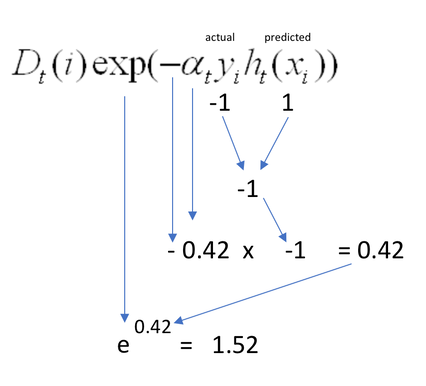
可以看到当弱分类器在某个样本上分类正确的时候，该样本的权重会降低；否则就会提升，符合理论预期。最后提一下$Z_t$，这是一个规范化系数（normalization factor ），是为了让新计算出来的权重代表一个真正的分布，一般就是归一化。比如上面的例子所有样本的权重更新后加起来后做一下归一化。上面的公式可以简化一下：

  • 对于分类正确的样本：$D_{t+1}(i)=\frac{D_t*e^{-\alpha_t}}{Z_t}$
  • 对于分类错误的样本：$D_{t+1}(i)=\frac{D_t*e^{\alpha_t}}{Z_t}$

最后一个问题，增加了预测错误的样本的权重之后，如何在下一轮迭代中更关注他们呢？实质是通过权重影响每一轮迭代数据集的选择来实现：比如我们有一个包含N个样本的数据集，每个样本都有一个权重（第一轮时权重相同，均为1/N），然后每一轮选择本轮使用的$m(m \le N)$个样本时，是根据权重随机采样的。也就是有些样本可能会被选择多次，有的可能一次也不会被选中。特别是当样本的权重被更新后，权重大的样本就更容易被选中，甚至选中多次了。这样这些样本自然会对后面的弱分类器产生比较多的影响。比如Pandas的sample方法就可以实现在一个数据集上面按照权重采样。

另外，还有一种“Bucket”的方式，思路如下：原来有N个样本，每次选N个样本进行弱学习器的训练。第一轮大家权重一样，第二轮的时候，根据权重先将原数据集划分“Bucket”，权重高的样本会占据多个bucket。而每个bucket被选中的几率是一样的，所以权重高的样本就可能被多选几次。也就是第二轮的时候虽然还是N个样本，但某些权重低的可能没有被选，某些权重高的样本可能被选了多次。比如下面的例子（N=5，ref：AdaBoost Algorithm – A Complete Guide for Beginners）:

第一轮，所有样本权重一样，可以理解为每个样本就是一个bucket：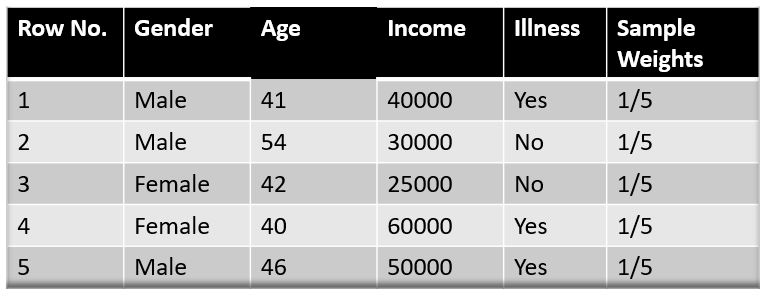
image.png

第一轮结束的时候，各个样本的权重已经发生了变化（假设第4条数据分错了，它的权重提升了）：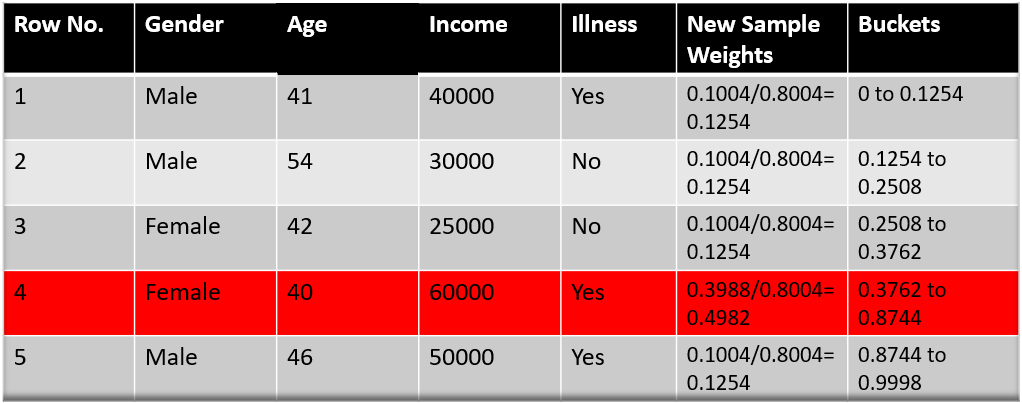
image.png

如上图，按照权重重新划分了数据集的bucket，分错的第2个样本占了比较多的bucket。所以在为第二轮迭代选择样本的时候，第4条被选中的概率就会比较大。比如算法随机的5个bucket是：0.38,0.26,0.98,0.40,0.55。那选出的样本就是下图：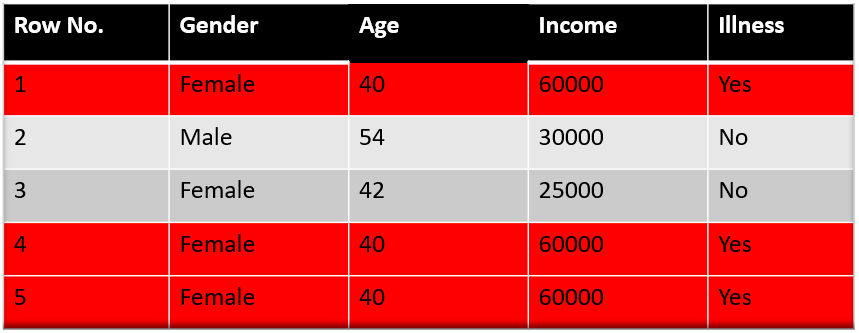
image.png

可以看到，样本4在第二轮出现了3次，这样后面的分类器必然会对该样本倾斜。

上面的第一种情况其实是后面bucket这种方式的一种特殊情况。所以，需要注意的是，每轮迭代改变了样本的权重后，对下一轮的影响是体现在挑选数据集的时候。当数据集选好后，这些数据集又会被赋予相同的权重，开始新一轮的迭代。后续不断按此方式迭代，直到错误率降到某个阈值或者达到预设的迭代次数。

例子

下面看两个例子，第一个偏理论，第二个偏实现，都有助于理解整个算法的流程和内在逻辑。

A Mathematical Explanation of AdaBoost in 5 Minutes

该例引用自：A Mathematical Explanation of AdaBoost in 5 Minutes。

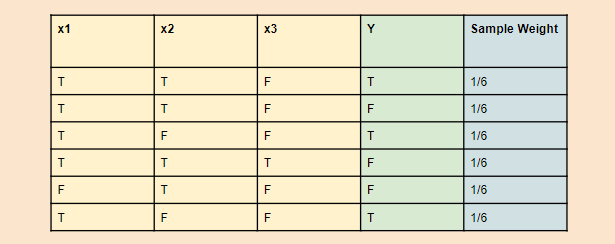
如下图：有一个包含6个样本的数据集，共3个属性：x1，x2，x3，输出为Y。其中T代表True，F代表False。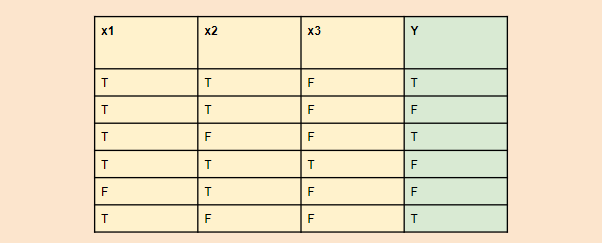
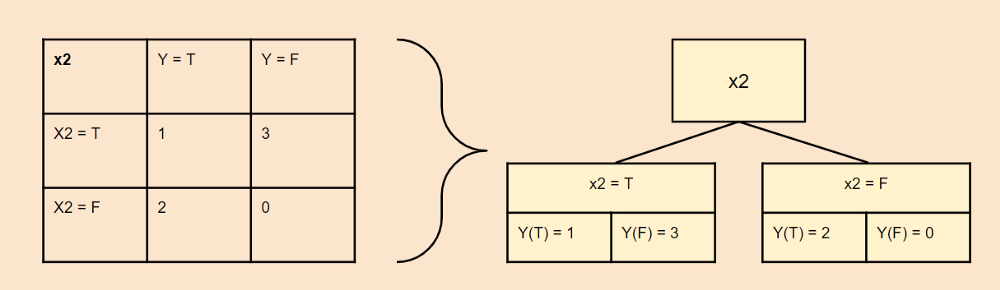
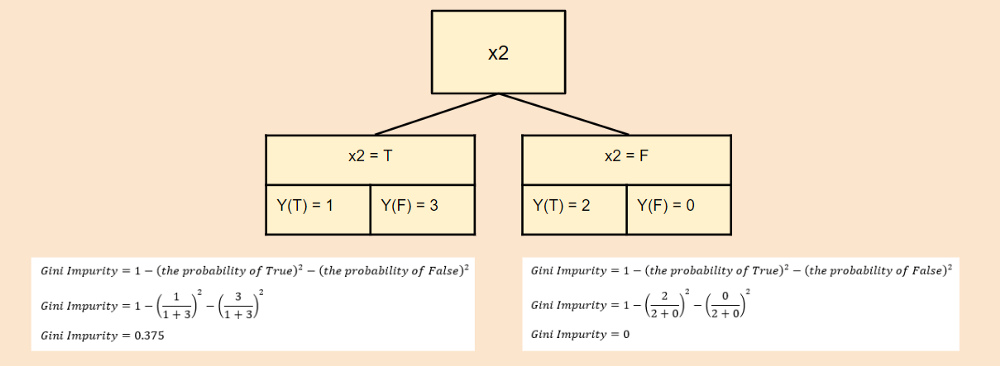
image.png

Step1：初始化，给每个样本赋予相同的权重，即1/6：
image.png

Step2：使用上面的数据生成弱学习器stump：分别计算各个属性的基尼不纯度（gini impurity）。

$$ Gini\ Impurity = 1- Pr_{true}^2-Pr_{false}^2 $$

这里以$x_2$属性为例进行计算：
image.png

image.png

$$ Total \ Impurity(x_2) = 0.375*(\frac{1+3}{6})+0*(\frac{2+0}{6}) = 0.25 $$

同理可以计算出$x_1$和$x_3$的不纯度为：

$$ Total\ Impurity(x_1)=(1-(\frac{2}{2+2})^2-(\frac{2}{2+2})^2)*(\frac{2+2}{6}) \\ + (1-(\frac{1}{1+0})^2-(\frac{0}{1+0})^2)*(\frac{1+0}{6}) \\ = 0.33 \\ \\ Total\ Impurity(x_3)=(1-(\frac{0}{0+1})^2-(\frac{1}{0+1})^2)*(\frac{0+1}{6}) \\ + (1-(\frac{3}{3+2})^2-(\frac{2}{3+2})^2)*(\frac{3+2}{6}) \\ = 0.4 $$

可以看到$x_2$的基尼不纯度最低，所以使用它生成第一个stump。

Step3：计算“amount of say”。使用x2属性生成的stump会将第1个样本分错，其它都正确。这样的话total error就是1/6。所以：

$$ Amount\ of\ say = \frac{1}{2}*log{\frac{1-\frac{1}{6}}{\frac{1}{6}}} = 0.35 $$

Step4：计算下一个弱分类器（stump）的样本权重。

  • 分类错误的样本新权重 $w_{incorrect} = \frac{1}{6}* e^{0.35} = 0.24$
  • 分类正确的样本新权重 $w_{correct} = \frac{1}{6}* e^{-0.35} = 0.12$

然后归一化得到下一个stump（即下一轮迭代）的样本及权重，如下图：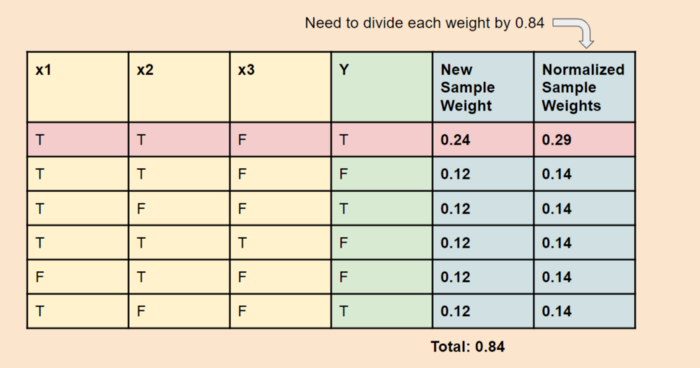
image.png

这样第一轮就结束了。第二轮迭代开始之前，要先根据样本权重选取训练数据，比如选择的样本可能如下（可以看到第一轮分类错误的样本这次被选了3次）：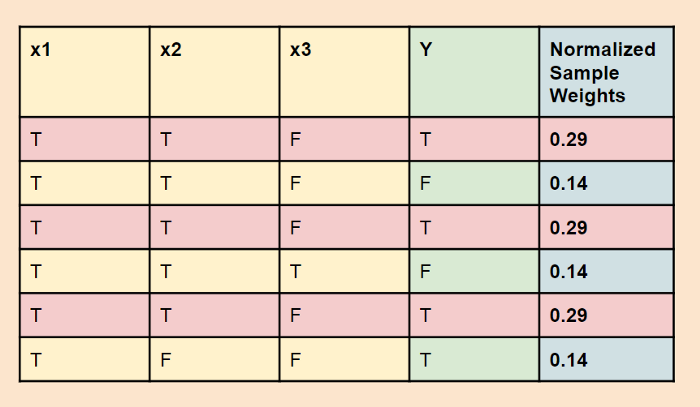
image.png

然后，将选中的样本权重初始化为相等的值，继续重复前面的过程：
image.png

直到训练误差足够小，或者弱分类器个数达到限制，则迭代终止。对所有弱分类器加权求和得到最终的强分类器。

Implementing the AdaBoost Algorithm From Scratch

上面的例子比较偏理论性，这个例子则是具体到代码实现层面的，限于篇幅和格式，就不在文章里面贴了。具体可以参见我的Github: implement-adaboost-from-scratch.ipynb。里面会根据上面的算法实现一个AdaBoost，并且最终和scikit-learn的AdaBoostClassifier做对比。
​
该例参考自：Implementing the AdaBoost Algorithm From Scratch

总结

AdaBoost算法的思想还是比较简单的，算法也容易理解，主要需要理解下面几个关键点：

  • 如何计算训练误差$\varepsilon_t$
  • 理解权重调整系数$\alpha_t$的作用
  • 样本权重是如何更新的，又是如何影响到下一轮迭代的

掌握了这些，在做模型的调优以及一些超参设置上也就可以游刃有余了。