GBDT
概述
GBDT全称Gradient Boosting Decision Trees,即梯度提升回归树。GBDT可以拆分2部分:GB+DT。GB是一种通用思想或者算法,GBDT只是众多GBM(Gradient Boosting Machine)里面的一种。所以先来看GB。
Boosting前面已经介绍过了,就是用多个弱学习器顺序迭代生成一个强学习器,GB里面的重点在于每次迭代的时候是拟合残差。所谓残差(residual)就是真实值和预测值的差值: $residual_i = y_i-f(x_i)$,它表示了数据模型中所不可能刻画的部分。所以GB的思想大致可以描述如下:
- 初始:先有一个初始的弱学习器,然后用这个学习器去训练样本上面进行预测,得到每个样本的残差。
- 第一轮:用训练样本作为属性,第一轮得到的残差作为target(而不是原始样本的target),训练得到第2个弱学习器。然后用这个弱学习器对样本进行预测得到预测值,并计算与真实值的残差,作为一下轮样本的target。
- 第N轮:重复前面的步骤。每次变化的是使用上一轮计算的残差作为本轮样本的target。
N次迭代后得到最终的强学习器。所以可以看到GB其实就是不断的迭代拟合残差。但至此并没有看到任何关于Gradient的影子。接着往下看:假设现在有样本集 $(x_1,y_1),(x_2,y_2),...(x_n,y_n)$ ,然后用一个模型$f(x)$去拟合这些数据。如果是回归模型的话,我们一般使用均方误差作为损失函数,即:$L(\theta) = \frac{1}{2}\sum_{i=0}^n(y_i-f(x_i))^2$
然后最优化算法求解模型的参数$\theta$。常用的最优化求解方法之一就是梯度下降(gradient descent)。对损失函数求梯度得到:$\nabla L(\theta) = \sum_{i=0}^n{(f(x_i)-y_i)}$
至此,可以看到我们前面定义的残差就是这里的负梯度:$residual_i = y_i-f(x_i) = -(f(xi)-y_i)$。也就是说前面对残差的拟合,其实就是对负梯度的拟合,而根据残差来更新集成后的模型实际就是根据负梯度来更新。这样来看,梯度提升方法就变成了广义上的梯度下降。这就是GB中Gradient的部分。
需要注意的是:尽管这里残差和负梯度的值完全一样,但二者代表的含义却是不一样的:负梯度指向的是单个模型参数更新的方向,残差(即梯度提升)则表示了集成模型下一个模型的拟合目标。梯度的不断下降可以让模型的参数逐渐收敛到最优参数上,而残差的不断拟合则让集成之后的模型越来越解决真实数据的生成机制。换言之,
- 梯度下降是参数空间的优化:针对单个模型的参数优化,找到最优的一组参数;
- 梯度提升是函数空间的优化:用多个模型的组合来逼近问题的解,每个模型都是一个函数。
有了从残差转换到梯度的思路以后,又可以再继续改进,不再局限于残差,而是可以从损失函数的负梯度角度去构造更丰富的提升方法,即构造更多的损失函数。因为基于残差的损失函数有一个明显的缺点就是对异常值比较敏感。看下面的例子:
上面的例子中,5*是一个异常点。很明显,按照Boosting的思路,后续模型会对这个值关注过多,这不是一个好现象。所以一般回归类的损失函数会使用绝对损失(absolute loss)或者huber损失函数(huber loss)来代替平方损失函数:
如果GB中的弱学习器使用决策树,就是GBDT了。GBDT中一般使用CART决策树。
这便是GBDT算法,整体还是Boosting的思路,但具体到细节又和AdaBoost有明显的差别:AdaBoost中每个弱学习器的短板通过权重的加强得以凸显,而梯度提升中则将权重换成了梯度。
在解决分类问题时,GBDT 中的负梯度可以表示成样本归属于每个类别的真实概率和上一轮预测概率的差值,这个差值会被回归树拟合,拟合值与上一轮预测概率求和就是这一轮的输出。
算法
下图来自Wikipedia:https://en.wikipedia.org/wiki/Gradient_boosting
初始化$F_0(x)$,表示第0棵树的预测值。那怎么初始化呢?取决于所选择的损失函数:
- 均方误差(mean square error,MSE)时:$F_0(x)=\bar y,\overline y$ 是样本真实值的平均值
- 平均绝对误差(mean absolute error,MAE):$F_0(x)=median(y)$,即真实值的中位数
- Logit时(分类问题): $F_0(x)=\frac{1}{2}*log\frac{\sum{y_i}}{\sum(1-y_i)}, y_i\in{0, 1}$
假如进行M轮迭代(即M个弱分类器),则对于第m轮($m=1,2,...,M$):
- 计算上一轮模型的残差(即负梯度)$r_{im}$,即用真实值减去上一轮模型的预测值
- 将计算出来的残差作为本轮的target,得到本轮的训练数据:$(x_1, r_{1m}),(x_2, r_{2m}),...,(x_n, r_{nm})$。然后训练得到本轮的弱分类器是$h_m(x)$。
- 然后就是求解本轮弱分类器的权重$\gamma_m$了。迭代到本轮为止得到的强分类器为:$F_m(x)=F_{m-1}(x)+\gamma_mh_m(x)$,所以求解$\gamma_m$的方式就是:$\gamma_m = \mathop{\arg\min}\limits_{\theta}\sum_{i=1}^n{L(y_i,F_m(x_i))} = \mathop{\arg\min}\limits_{\theta}\sum_{i=1}^n{L(y_i,F_{m-1}(x_i)+\gamma h_m(x_i))}$
- 得到$\gamma_m$之后,本轮迭代之后得到模型就是:$F_m(x)=F_{m-1}(x)+\gamma_mh_m(x)$。
- 得到最终的模型:$F_M(x)$。
再总结一下关键点:
- 初始的时候先找一个常量模型$F_0$,计算初始的残差。之所以说是常量模型,是因为一般这个是直接计算的所有样本观测值(target)的“均值”(如果是分类问题的话,一般使用logit),然后样本观测值减去计算出来的“均值”就得到了初始的残差。然后就开始Boosting的迭代,每轮迭代的样本属性就是原始训练样本的属性,但样本观测值不是原始的观测值,而是计算出来的残差。第一轮使用初始算出的残差;第二轮使用第一轮模型预测的到的残差,...,第m轮使用第m-1轮模型预测得到的残差,以此类推。
- 因为Boosting模型得到的最终强学习器形式为:$F_{strong\ learner}(x) = \sum_{i=1}^M{\gamma_i*h_i(x)} +const_{F_0}$
其中的$const_{F_0}$就是初始计算的常量“均值”,所以每轮除了使用样本$(x_1, r_{1m}),(x_2, r_{2m}),...,(x_n, r_{nm})$ 训练得到本轮的弱分类器以外,还需要计算本轮弱分类器在最终强分类器中所占的权重$\gamma$,计算方式就是上面计算$\gamma_m$的方法。 - 需要注意的是每轮训练时的target使用的是残差,而不是原始的target,所以该弱分类器模型后面预测出来的值也是残差,而不是原始样本的target。也即所以上面公式中的$\sum_{i=1}^M{\gamma_i*h_i(x)}$累加起来其实是M个弱分类器预测的“残差和”,需要加上最初始$F_0$算出来的“平均值”才是最终的预测值。
另外还需要说明一个概念:学习率(Learning Rate),背景是这样的:测试表明每次沿正确的方向前进一小步可以获得更好的预测性能,所以设计了一个超参learning rate,用来控制每轮模型的影响。一般会设置的比较小(比如0.1),以此来让模型使用更多的弱分类器。英文版:
It’s been shown through experimentation that taking small incremental steps towards the solution achieves a comparable bias with a lower overall vatiance (a lower variance leads to better accuracy on samples outside of the training data). Thus, to prevent overfitting, we introduce a hyperparameter called learning rate. When we make a prediction, each residual is multiplied by the learning rate. This forces us to use more decision trees, each taking a small step towards the final solution.
上面的算法流程里面没有给出来,但实际迭代的时候还会引入一个学习率$\nu$,完整的迭代公式是这样的:$F_m(x)=F_{m-1}(x)+\nu*\gamma_mH_m(x)$
一幅图表示就是(来自:How XGBoost Works):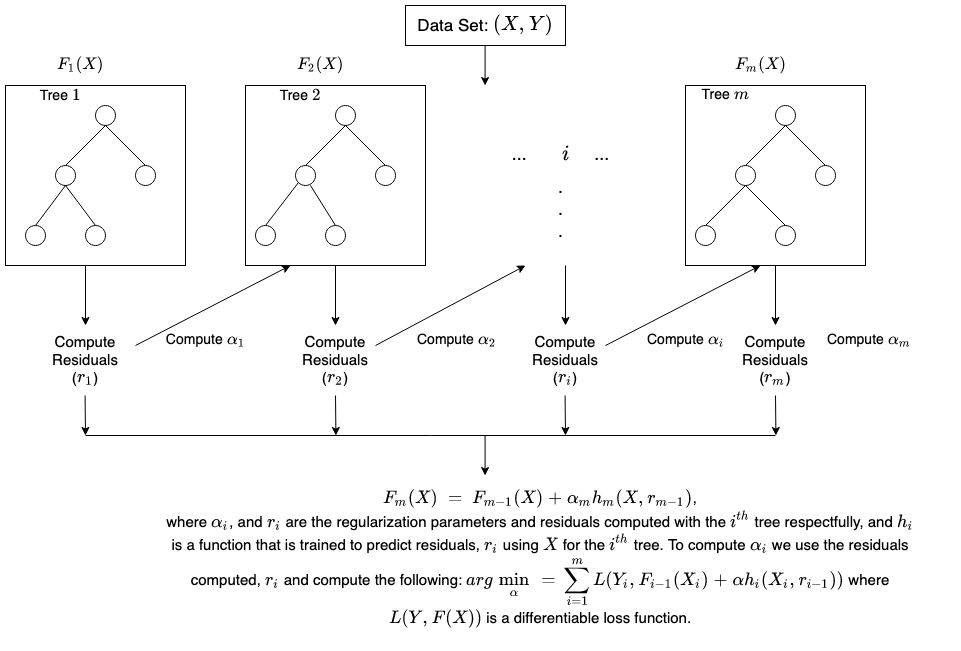
整个介绍起来比较抽象,可参考下面例子中的第一个:Gradient Boosting Decision Tree Algorithm Explained来感受一下整个流程。
例子
- Gradient Boosting Decision Tree Algorithm Explained: 该例是一个使用GBDT解决回归的问题。见:gbdt-regression-demo.ipynb(参考自: Gradient Boosting Decision Tree Algorithm Explained)。
- GBDT算法原理以及实例理解
- Gradient Boosting In Classification: Not a Black Box Anymore!,是一个二分类例子。
XGBoost
概述
XGBoost(eXtreme Gradient Boosting)是对GBDT的优化和工程化的实现。优化可分为算法优化和工程实现方面的优化:
Algorithmic Enhancements:
- Regularization: It penalizes more complex models through both LASSO (L1) and Ridge (L2) regularization to prevent overfitting.
- Sparsity Awareness: XGBoost naturally admits sparse features for inputs by automatically ‘learning’ best missing value depending on training loss and handles different types of sparsity patterns in the data more efficiently.
- Weighted Quantile Sketch: XGBoost employs the distributed weighted Quantile Sketch algorithm to effectively find the optimal split points among weighted datasets.
- Cross-validation: The algorithm comes with built-in cross-validation method at each iteration, taking away the need to explicitly program this search and to specify the exact number of boosting iterations required in a single run.
System Optimization:
- Parallelization: XGBoost approaches the process of sequential tree building using parallelized implementation. This is possible due to the interchangeable nature of loops used for building base learners; the outer loop that enumerates the leaf nodes of a tree, and the second inner loop that calculates the features. This nesting of loops limits parallelization because without completing the inner loop (more computationally demanding of the two), the outer loop cannot be started. Therefore, to improve run time, the order of loops is interchanged using initialization through a global scan of all instances and sorting using parallel threads. This switch improves algorithmic performance by offsetting any parallelization overheads in computation.
- Tree Pruning: The stopping criterion for tree splitting within GBM framework is greedy in nature and depends on the negative loss criterion at the point of split. XGBoost uses ‘max_depth’ parameter as specified instead of criterion first, and starts pruning trees backward. This ‘depth-first’ approach improves computational performance significantly.
Hardware Optimization: This algorithm has been designed to make efficient use of hardware resources. This is accomplished by cache awareness by allocating internal buffers in each thread to store gradient statistics. Further enhancements such as ‘out-of-core’ computing optimize available disk space while handling big data-frames that do not fit into memory.
算法
从算法角度来说,XGBoost主要对GBDT的目标函数进行了优化。GBDT的目标函数:
$Obj_{gbdt} = \sum_{i=1}^N{L(f_m(x_i), y_i)}=\sum_{i=1}^N{L(f_{m-1}(x_i) + h_m(x_i), y_i)}$
而XGBoost对目标函数的优化有两方面:
- 加了一个正则项;
- 使用泰勒公式展开。
先看正则项:
$Obj_{xgboost} = \sum_{i=1}^N{L(f_m(x_i), y_i)} + \sum_{j=1}^m{\Omega f(x_j)}=\sum_{i=1}^N{L(f_{m-1}(x_i) + h_m(x_i), y_i) + \sum_{j=1}^m{\Omega f(x_j)}}$
加正则项就是Shrinkage的思想,可以防止过拟合、降低方差,获取更好的泛化效果。这个正则项的具体公式为:
$\Omega f(x_i) = \gamma T + \frac{1}{2}\lambda||\omega||^2$
其中$T$为树$f$的叶节点个数,$\omega$为所有叶节点输出回归值构成的向量,$\gamma,\lambda$为超参数。再看泰勒公式:
更细的部分可参考下面2篇文章:
- 机器学习|XGBoost详解(CSDN)
- XGBooost详解(知乎)
总结
梯度提升算法(Gradient Boosting Machine,GBM)其实是一类算法,GBDT只是其中一种,而XGBoost则是GBDT的一个优化版本(或者说是GBDT算法的一个具体的实现),这个优化不仅体现在算法层面,也包括很多工程实现方面的优化,比如并行、内存使用量少等。同类的还有微软开源的LightGBM,号称速度更快,内存使用更低,网上有很多对比评测文章,有兴趣的可以看看。
 NYC's Blog
NYC's Blog 
评论已关闭