注:本文基于Lucene 8.2.0 版本。
本文是Lucene系列的终篇,在这篇文章中,我们会简单聊一下Lucene的相似度评分机制。
TF-IDF
Bag-of-words模型
先介绍一下NLP和IR领域里面非常简单且使用极其广泛的bag-fo-words model,即词袋模型。假设有这么一句话:"John likes to watch movies. Mary likes movies too."。那这句话用JSON格式的词袋模型表示的话就是:
BoW = {"John":1,"likes":2,"to":1,"watch":1,"movies":2,"Mary":1,"too":1};可以看到,词袋模型关注的是词的出现次数,而没有记录词的位置信息。所以不同的语句甚至相反含义的语句其词袋可能是一样的,比如"Mary is quicker than John"和"John is quicker than Mary"这两句话,其词袋是一样的,但含义是完全相反的。所以凡是完全基于词袋模型的一些算法一般也存在这样该问题。
Term frequency
词频就是一个词(term)在一个文档中(document)出现的次数(frequency),记为 $tf_{t,d}$。这是一种最简单的定义方式,实际使用中还有一些变种:
- 布尔词频:如果词在文档中出现,则 $tf_{t,d}=1$,否则为0。
- 根据文档长短做调整的词频:$tf_{t,d}/length$,其中length为文档中的总词数。
- 对数词频:$log(1+tf_{t,d})$,加1是防止对0求对数(0没有对数)。 一般选取常用对数或者自然对数。
词频的优点是简单,但缺点也很显然:
- 词频中没有包含词的位置信息,所以从词频的角度来看,"Mary is quicker than John"和"John is quicker than Mary"两条文档是完全一致的,但显然它们的含义是完全相反的。
- 词频没有考虑不同词的重要性一般是不一样的,比如停用词的词频都很高,但它们并不重要。
Inverse document frequency
一个词的逆文档频率用于衡量该词提供了多少信息,计算方式定义如下:
$$ idf_t = log\frac{N}{df_t}=-log\frac{df_t}{N} $$
其中,$t$ 代表term,$D$ 代表文档,$N$ 代表语料库中文档总数,$df_t$ 代表语料库中包含 $t$ 的文档的数据,即文档频率(document frequency)。如果语料库中不包含 $t$,那 $df_t$ 就等于0,为了避免除零操作,可以采用后面的公式,将 $df_t$ 作为分子,也有的变种给 $df_t$ 加了1.
对于固定的语料库,N是固定的,一个词的 $df_t$ 越大,其$idf(t, D)$ 就越小。所以那些很稀少的词的 $idf$ 值会很高,而像停用词这种出现频率很高的词 $idf$ 值很低。
TF-IDF
TF-IDF就是将TF和IDF结合起来,其实就是简单的相乘:
$$ tfidf(t, d)=tf_{t,d} \cdot idf_t $$
从公式可以分析出来,一个词 $t$ 在某个文档 $d$ 中的tf-idf值:
- 当该词在少数文档中出现很多次的时候,其值接近最大值;(场景1)
- 当该词在文档中出现次数少或者在很多文档中都出现时,其值较小;(场景2)
- 当该词几乎在所有文档中都出现时,其值接近最小值。(场景3)
下面用一个例子来实战一下,还是以《Lucene系列(2)——代码实践》文中的4首英文短诗中的前3首为例。假设这3首诗组成了我们的语料库,每首诗就是一个文档(doc1:Fog、doc2:Freedom And Love、doc3:Love's Secret),诗里面的每个单词就是一个个词(我们把标题也包含在里面)。然后我们选取"the"、 "freedom"、"love"三个词来分别计算它们在每个文档的TF-IDF,计算中使用自然对数形式。
"the"在doc1中出现了1次,在doc2中出现了2次,在doc3中出现了1次,整个语料库有3个文档,包含"the"的文档也是3个。所以:
- doc1: $tf=ln(1+1), idf=ln\frac{3}{3}, tfidf("the","doc1")= tf \cdot idf =ln2 \cdot ln1=0$
- doc2: $tf=ln(1+2), idf=ln\frac{3}{3}, tfidf("the","doc2")=tf \cdot idf=ln3 \cdot ln1=0$
- doc3: $tf=ln(1+1), idf=ln\frac{3}{3}, tfidf("the","doc3")=tf \cdot idf=ln2 \cdot ln1=0$
"freedom"在doc1中出现了0次,在doc2中出现了1次,在doc3中出现了0次,语料库中包含"freedom"的文档只有1个。所以:
- doc1: $tf=ln(1+0), idf=ln\frac{3}{1}, tfidf("freedom","doc1")= tf \cdot idf =ln1 \cdot ln3=0$
- doc2: $tf=ln(1+1), idf=ln\frac{3}{1}, tfidf("freedom","doc2")= tf \cdot idf =ln2 \cdot ln3=0.76$
- doc3: $tf=ln(1+0), idf=ln\frac{3}{1}, tfidf("freedom","doc3")= tf \cdot idf =ln1 \cdot ln3=0$
"love"在doc1中现了0次,在doc2中出现了3次,在doc3中出现了5次,整个语料库有3个文档,包含"love"的文档有2个。所以:
- doc1: $tf=ln(1+0), idf=ln\frac{3}{2}, tfidf("love","doc1")= tf \cdot idf =ln1 \cdot ln\frac{3}{2}=0$
- doc2: $tf=ln(1+3), idf=ln\frac{3}{2}, tfidf("love","doc2")= tf \cdot idf =ln4 \cdot ln\frac{3}{2}=0.56$
- doc3: $tf=ln(1+5), idf=ln\frac{3}{2}, tfidf("love","doc3")= tf \cdot idf =ln6 \cdot ln\frac{3}{2}=0.73$
我们简单分析一下结果:"the"在所有文档中都出现了,所以其tf-idf值最低,为0,验证了上面公式分析中的场景3;"freedom"只有在第2个文档中出现了,所以其它两个的tf-idf值为0,表示不包含该词;"love"在第2、3个文档中都出现了,但在第3个文档中出现的频率更高,所以其tf-idf值最高。所以tf-idf算法的结果还是能很好的表示实际结果的。
Vector Space Model
通过TF-IDF算法,我们可以计算出每个词在语料库中的权重,而通过VSM(Vector Space Model),则可以计算两个文档的相似度。
假设有两个文档:
- 文档1:"Jack Ma regrets setting up Alibaba."
- 文档2:"Richard Liu does not know he has a beautiful wife."
这是原始的文档,然后通过词袋模型转化后为:
- BoW1 = {"jack":1, "ma":1, "regret":1, "set":1, "up":1, "alibaba":1}
- BoW2 = {"richard":1, "liu":1, "does":1, "not":1, "know":1, "he":1, "has":1, "a": 1, "beautiful":1, "wife":1}
接着,分别用TF-IDF算法计算每个文档词袋中每个词的tf-idf值(值是随便写的,仅供原理说明):
- tf-idf_doc1 = { 0.41, 0.12, 0.76, 0.83, 0.21, 0.47 }
- tf-idf_doc2 = { 0.12, 0.25, 0.67, 0.98, 0.43, 0.76, 0.89, 0.51, 0.19, 0.37 }
如果将上面的tf-idf_doc1和tf-idf_doc2看成是2个向量,那我们就通过上面的方式将原始的文档转换成了向量,这个向量就是VSM中的Vector。在VSM中,一个Vector就代表一个文档(记为 $V(q)$),Vector中的每个值就是原来文档中term的权重(这个权重一般使用tf-idf计算,也可以通过其他方式计算)。这样语料库中的很多文档就会产生很多的向量,这些向量一起构成了一个向量空间,也就是Vector Space。
假设有一个查询语句为"Jack Alibaba",我们可以用同样的方式将其转化一个向量,假设这个向量叫查询向量 $V(q)$。这样在语料库中检索和 $q$ 相近文档的问题就转换成求语料库中每个向量 $V(d)$ 与 $V(q)$ 的相似度问题了。而衡量两个向量相似度最常用的方法就是余弦相似度(Cosine similarity),以下内容来自维基百科:
余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1,而其他任何角度的余弦值都不大于1;并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时,余弦相似度的值为1;两个向量夹角为90°时,余弦相似度的值为0;两个向量指向完全相反的方向时,余弦相似度的值为-1。这结果是与向量的长度无关的,仅仅与向量的指向方向相关。余弦相似度通常用于正空间,因此给出的值为0到1之间。
用公式表示就是:
$$ cosineSimilarity(q,d)=\frac{V(q) \cdot V(d)}{|V(q)||V(d)|}=v(q) \cdot v(d) $$
其中,$V(q)$是查询向量,$V(d)$是文档向量,$|V(q)|$和$|V(q)|$是两个向量的长度,$v(q)$和$v(q)$则是对应的单位向量。
这个就是Vector Space Model。
TFIDFSimilarity
Lucene使用Boolean model (BM) of Information Retrieval模型来计算一个文档是否和搜索词匹配,对于匹配的文档使用基于VSM的评分算法来计算得分。具体的实现类是org.apache.lucene.search.similarities.TFIDFSimilarity,但做了一些修正。本文不讨论BM算法,只介绍评分算法。TFIDFSimilarity采用的评分公式如下:
$$ Score(q, d)=\sum_{t\in q}(tf_{t, d} \cdot {idf_t}^2 \cdot t.getBoost() \cdot norm(t, d)) $$
我们从外到内剖析一下这个公式。
- 最外层的累加。搜索语句一般是由多个词组成的,比如"Jack Alibaba"就是有"Jack"和"Alibaba"两个词组成。计算搜索语句和每个匹配文档的得分的时候就是计算搜索语句中每个词和匹配文档的得分,然后累加起来就是搜索语句和该匹配文档的得分。这就是最外层的累加。
- $t.getBoost()$。之前的系列文章中介绍过,在查询或者索引阶段我们可以人为设定某些term的权重,t.getBoost()获取的就是这个阶段设置的权重。所以查询或索引阶段设置的权重也就是在这个时候起作用的。
$norm(t, d)$。之前的系列文章中也介绍过,查询的时候一个文档的长短也是会影响词的重要性,匹配次数一样的情况下,越长的文档评分越低。这个也好理解,比如我们搜"Alibaba",有两个文档里面都出现了一次该词,但其中一个文档总共包含100万个词,而另外一个只包含10个词,很显然,极大多数情况下,后者与搜索词的相关度是比前者高的。实际计算的时候使用的公式如下:
$$ norm(t,d) = \frac{1}{\sqrt{length}} $$
其中 $length$是文档 $d$ 的长度。
$tf_{t, d} \cdot {idf_t}^2$。Lucene假设一个词在搜索语句中的词频为1(即使出现多次也不影响,就是重复计算多次而已),所以可以把这个公式拆开写:
$$ tf_{t, d} \cdot {idf_t}^2 = tf_{t, d} \cdot {idf_t} \cdot 1 \cdot {idf_t}=(tf_{t, d} \cdot {idf_t}) \cdot (tf_{t, q} \cdot {idf_t}) $$
这里的$(tf_{t, d} \cdot {idf_t}) \cdot (tf_{t, q} \cdot {idf_t})$就对应上面的$v(d) \cdot v(q)$.
在Lucene中,采用的TF计算公式为:
$$ tf_{t,d} = \sqrt {frequency} $$
IDF计算公式为:
$$ idf_t =1+log\frac{N+1}{df_t+1} $$
其实TFIDFSimilarity是一个抽象类,真正实现上述相似度计算的是org.apache.lucene.search.similarities.ClassicSimilarity类,上面列举的公式在其对应的方法中也可以找到。除了基于TFIDF这种方式外,Lucene还支持另外一种相似度算法BM25,并且从6.0.0版本开始,BM25已经替代ClassicSimilarity,作为默认的评分算法。下面就来看看BM25.
BM25Similarity
BM25全称“Best Match 25”,其中“25”是指现在BM25中的计算公式是第25次迭代优化。该算法是几位大牛在1994年TREC-3(Third Text REtrieval Conference)会议上提出的,它将文本相似度问题转化为概率模型,可以看做是TF-IDF的改良版,我们看下它是如何进行改良的。
对IDF的改良
BM25中的IDF公式为:
$$ idf_t^{BM25} = log(1+\frac{N-df_t+0.5}{df_t+0.5}) $$
注意:原版BM25的log中是没有加1的,Lucene为了防止产生负值,做了一点小优化。
虽然对公式进行了更改,但其实和原来的公式没有实质性的差异,下面是新旧函数曲线对比:
对TF的改良1
BM25中TF的公式为:
$$ tf_{t,d}^{BM25}=((k+1)*tf)/(k+tf) $$
其中$tf$是传统的词频值。先来看下改良前后的函数曲线对比吧(下图中$k=1.2$):
可以看到,传统的tf计算公式中,词频越高,tf值就越大,没有上限。但BM中的tf,随着词频的增长,tf值会无限逼近$(k+1)$,相当于是有上限的。这就是二者的区别。一般 $k$ 取 1.2,Lucene中也使用1.2作为 $k$ 的默认值。
对TF的改良2
在传统的计算公式中,还有一个norm。BM25将这个因素加到了TF的计算公式中,结合了norm因素的BM25中的TF计算公式为:
$$ tf_{t,d}^{BM25}=((k+1)*tf)/(k*(1.0-b+b*L)+tf) $$
和之前相比,就是给分母上面的 $k$ 加了一个乘数 $(1.0-b+b*L)$. 其中的 $L$ 的计算公式为:
$$ L = \frac{|d|}{avgDl} $$
其中,$|d|$是当前文档的长度,$avgDl$ 是语料库中所有文档的平均长度。
$b$ 是一个常数,用来控制 $L$ 对最总评分影响的大小,一般取0~1之间的数(取0则代表完全忽略 $L$ )。Lucene中 $b$ 的默认值为 0.75.
通过这些细节上的改良,BM25在很多实际场景中的表现都优于传统的TF-IDF,所以从Lucene 6.0.0版本开始,上位成为默认的相似度评分算法。
 NYC's Blog
NYC's Blog 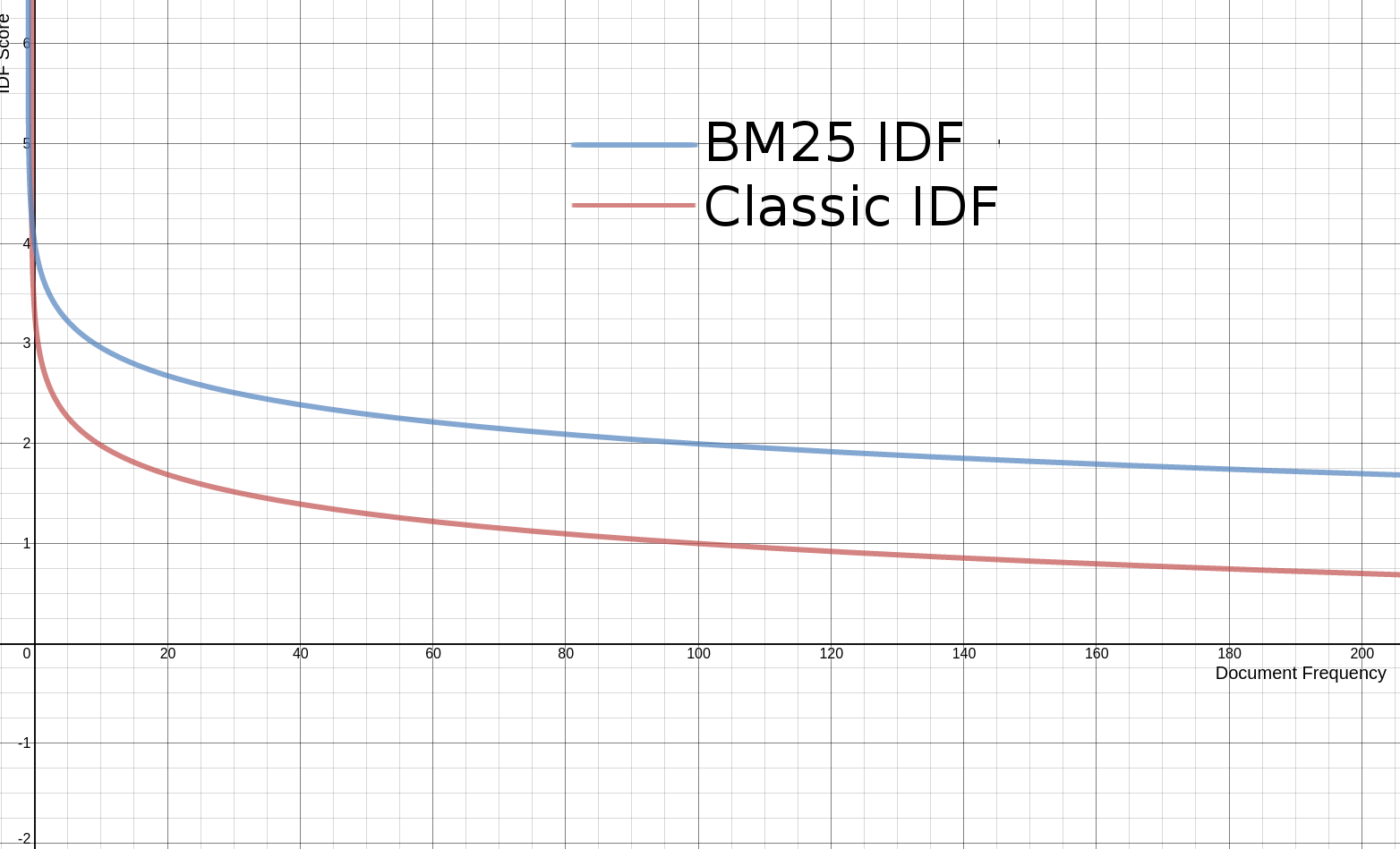

评论已关闭